Thermodynamic and Kinetic Modeling of Hydrogen Storage Materials Microstructures
Category
Modeling/Simulation
Laboratory
Lawrence Livermore National Laboratory (LLNL)
Capability Expert
Tae Wook Heo ([email protected])
Description
The hydrogen storage performance and reversibility are often influenced by the thermodynamics and kinetics of phase transformations and associated microstructures of the storage materials. In this regard, this modeling and simulation capability within HyMARC provides the foundational understanding of physical mechanisms leading to different types of mesoscale phase microstructures of solid-state hydrogen storage materials involving multiple intermediates. This is essential for identifying the rate-limiting processes of (de/re)hydrogenation in order to predict and improve the hydrogen storage performance/reversibility. In particular, we have been developing and applying two multiscale simulation capabilities:
- Thermodynamic calculation method for predicting intermediate/product phase fractions
- Phase-field modeling method for simulating kinetic phase microstructure/transformation behaviors.
The thermodynamic phase fraction calculation method is based on the fundamental thermodynamic principles for the mixture of multiple phases and components. By finding the phase fractions that minimize the total free energy of the mixture incorporating the interfacial/surface energy effects, we analyze the thermodynamic intermediate/product phase behaviors for the given H2 pressure, temperature, and particle sizes. Figure 1 illustrates the framework of this method and shows an example of the application to a Li-N-H system. The phase-field modeling (PFM) uses a continuum description to simulate non-equilibrium kinetics and phase evolution across broad ranges of time and length scales. It has been identified as one of the most powerful computational methods for modeling microstructure evolution owing to its simplicity and flexibility to describe the complicated configuration of microstructures. Figure 2 shows the illustration of its general framework and application to a Pd-H system. For quantitative modeling, both methods are parameterized by materials parameters and thermodynamic energetics (e.g., elastic modulus, lattice parameter, interfacial energy, free energy) derived from either atomistic/thermodynamic calculations or experiments by LLNL/SNL/LBNL. These techniques are quite general and applicable to various classes of hydrogen storage materials, for example, ranging from simple interstitial hydrides to complex metal hydrides.
Unique Aspects
The phase microstructure evolution of hydrogen storage materials usually involves phase transformations in the presence of structural and/or elastic inhomogeneities (e.g., surfaces, grain boundaries) as well as anisotropies. The recent advances of the phase-field method to elastically/structurally inhomogeneous and anisotropic materials [1–5] enable the modeling of kinetic materials processes such as mass transport and crystallographic structural transformations in polycrystalline materials, which is more realistic in actual hydrogen storage applications.
Availability/Status
Since the necessary phase-field models [1–5] of fundamental materials processes for describing relevant materials phenomena in hydrogen storage materials are available at LLNL, the models/codes can be integrated and adapted by the LLNL capability experts to simulate microstructure evolution and materials processes of the specific hydrogen storage materials of interest. Furthermore, the extensive development of relevant phase-field models/codes as well as the phase fraction calculation codes for several representative hydrides are underway within HyMARC. Later, we expect that the phase-field codes based on more efficient and scalable LLNL AMPE (Adaptive Mesh Phase Evolution) code for specific hydrogen storage materials will be available to the hydrogen storage community.
Figures
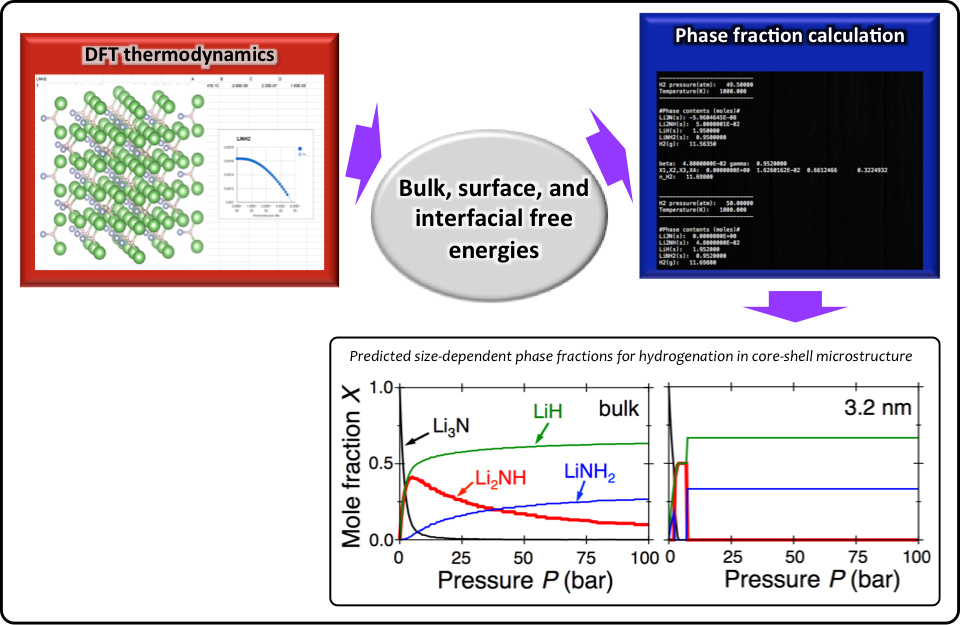
Figure 1. Thermodynamic phase fraction calculation framework and its application to Li-N-H.
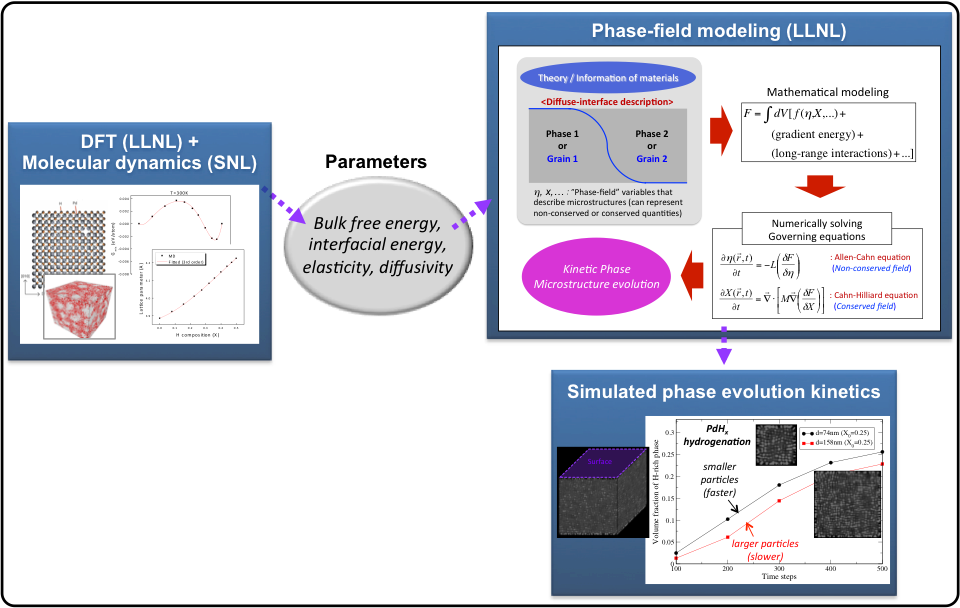
Figure 2. Phase-field modeling/simulation framework and its application to Pd-H.
References
- T.W. Heo, S. Bhattacharyya, and L.-Q. Chen, Acta Materialia 59 (2011): 7800.
- T.W. Heo, S. Bhattacharyya, and L.-Q. Chen, Philosophical Magazine 93 (2013): 1468.
- T.W. Heo and L.-Q. Chen, Acta Materialia 76 (2014): 68.
- T.W. Heo, L.-Q. Chen, B.C. Wood, Computational Materials Science 108 (2015): 323.
- T.W. Heo, M. Tang, L.-Q. Chen, and B.C. Wood, Advanced Energy Materials 6 (2016): 1501759.
