Ab Initio Calculation Capabilities for Hydrogen Storage Materials
Category
Modeling/Simulation
Laboratory
Lawrence Livermore National Laboratory (LLNL)
Capability Experts
Brandon C. Wood ([email protected]), Miguel A. Morales ([email protected]), Keith G. Ray ([email protected]), ShinYoung Kang ([email protected]), Stanimir A. Bonev ([email protected]), Tadashi Ogitsu ([email protected])
Description
At LLNL, we have access to an incredibly diverse toolkit for modeling hydrogen storage materials with first-principles quantum mechanical calculations. These calculations allow for the determination of the thermodynamic and kinetic properties of hydrogen storage materials without the need for empirical parameters. Here we highlight our computational resources and our expertise as it relates to our capability to perform calculations on many different levels of accuracy/included physics and system size. In particular, our capabilities include:
- Quantum Monte Carlo (QMC) and advanced density functionals
- Finite-temperature thermodynamic free energy calculations
- Large-scale ab initio molecular dynamics (AIMD) calculations
- Computational X-ray spectroscopy.
The QMC method is a computationally intensive yet highly accurate quantum many-body method that can be used to refine energetics of sorbents at beyond-DFT accuracies [1, 2]. Within HyMARC, QMC is used to accurately compute binding energy curves for the interaction of H2 with MOF- and carbon-based sorbents, which in turn will be used to construct absorption isotherms and compile a database.
Our AIMD simulation capability (see Figure 1) can deal with systems containing more than 1,000 atoms making it possible to investigate relevant systems for hydrogen storage research such as surfaces, interfaces, and disordered systems. The relevant codes also offer various types of constrained MD, which enable us to investigate the reaction kinetics of hydrogen charging/discharging processes, in addition to thermodynamic properties of the storage materials in various stages. These simulations provide input information for meso-scale code addressing longer-time and length scale phenomena.
In order to identify hydrogen storage materials using experimental X-ray absorption spectra from unknown phases and compounds, we can simulate XAS spectra using DFT performed on candidate known phases in collaboration with LBNL. Not only useful for identification, such studies elucidate the electronic structure and binding chemistry/geometry as a material is hydrogenated.
Temperature-dependent phase transitions are usually entropy-driven. Large entropic contributions to the free energy of a solid (see Figure 2) imply low-frequency lattice modes, which are likely to be anharmonic. We use vibrational density of states from molecular dynamics simulations, which represent temperature-renormalized phonons, to capture the anharmonic contributions to the thermodynamics of hydrides. In addition to being efficient, the method allows us to identify contributions from specific atoms, regions of space, or normal modes [3]. For a strongly diffusive subsystem, the entropy can be estimated within a few percent accuracy using a gas-solid model for liquid entropy [4].
Unique Aspect
At LLNL, we have experience with ab initio calculations in a variety of formalisms. We employ density functional theory (DFT) with several different functionals to include interactions that are often neglected, such as van der Waals interactions captured by the vdW-DF, or to remedy inaccuracies, such as self-interaction errors that can be mitigated with a hybrid functional. These are important for dealing with systems with weak binding or highly correlated/localized electrons, respectively, when calculating thermodynamic or kinetic properties of hydrogen storage materials. This capability is on line. We also can perform quantum Monte Carlo (QMC) calculations. While QMC calculations are much more computationally expensive, compared to DFT, the accuracy is greater and all interactions are included. This capability can be useful to benchmark other techniques for difficult or new systems. We emphasize that all these large scale and computationally expensive quantum mechanical simulations can be efficiently executed owing to LLNL’s leadership-class supercomputing facilities (two of the world’s ten fastest) and highly optimized quantum modeling codes.
Availability/Status
For quantum mechanical simulations, we extensively use the following codes:
In particular, with recent software and hardware developments, QMC can study unit cells with up to 500 atoms (including H2 in MOFs) utilizing QMCPACK [5], a modern open-source code co-developed by Dr. Miguel Morales at LLNL and optimized for large-scale execution (>90% scaling efficiency) on the petascale computing resources at LLNL. The code offers state-of-the-art implementations of current and emerging QMC algorithms, including real-space, orbital-base routines that can access large system sizes [6, 7].
The AIMD runs will leverage the highly scalable Qbox and Qb@ll code developed at LLNL and also optimized for the leadership-class computing facilities. These codes were developed in the Midwest Integrated Center for Computational Materials (MICCoM). Qbox is the original version of qb@ll developed by then staff scientist Francois Gygi (currently at University of California Davis) with the assistance of Dr. Erik Draeger of CASC/LLNL, who is developing/maintaining qb@ll. Thanks to Prof. Gygi and Dr. Draeger, the codes can take full advantage of the complex and sophisticated modern supercomputers (winner of 2006 Gordon Bell Prize for its sustained peak performance). A very recent development is the implementation of a virtual potentiostat into Qb@ll AIMD, which allows us to simulate processes at finite voltage bias. The codes have been run on the state-of-art supercomputers such as BGL/BGQ as well as on Linux cluster based supercomputers for real-world research projects for more than a decade.
Figures

Figure 1. AIMD snapshot
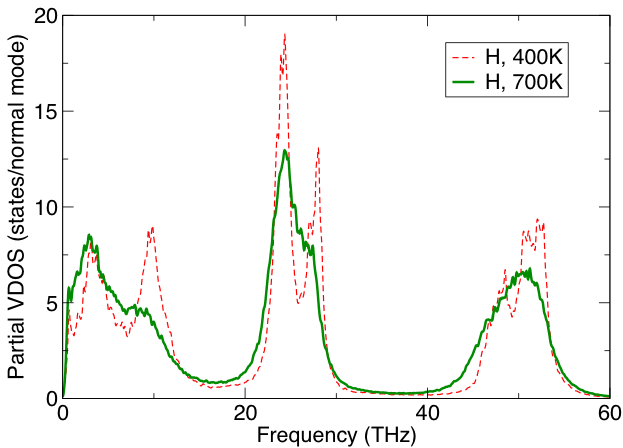
Figure 2. Vibrational density of states of the hydrogen subsystem in a Mg(BH4)2 solid. The entropy is dominated by the low-frequency modes (below 20 THz), which are clearly anharmonic. The entropic contribution to the free energy at 700 K is 220 mev/atom, of which 135 mev/atom is due to H, with about 13% due to anharmonic effects. Such quantities are significant when predicting phase stability.
References
- W. Foulkes, L. Mitas, R. Needs, and G. Rajagopal, Rev. Mod. Phys. 73 (2001): 33.
- M. S. Dubecky, P. Jurecka, R. Derian, P. Hobza, M. Otyepka, and L. Mitas, J. Chem. Theory Comput. 9 (2013): 4287.
- A. M. Teweldeberhan, J.L. Dubois, and S.A. Bonev, Phys. Rev. Lett. 105 (2010): 235503.
- A. M. Teweldeberhan and S.A. Bonev, Phys. Rev. B 83 (2011): 134120.
- J. Kim, K. Esler, J. McMinis, M. A. Morales, B. Clark, J. Gergely, S. Chiesa, K. Delaney, J. Vincent, and D. Ceperley, www.qmcpack.org (2014).
- J. Kim, K. P. Esler, J. McMinis, M. A. Morales, B. K. Clark, L. Shulenburger, D. M. Ceperley, In J. Phys.: Conf. Ser. 402 (2012): 012008.
- M. A. Morales, J. McMinis, B. K. Clark, J. Kim, G. E. Scuseria, J. Chem. Theory Comp. 8 (2012): 2181.
