Atomistic Simulations of Hydrogen Transport in Materials

Category

Modeling/Simulation

Description

Within the computational framework of HyMARC, we have strong capabilities of developing high-fidelity interatomic potentials for new materials of interest, and using large scale molecular dynamics (MD) and kinetic Monte Carlo (kMC) simulations enabled by Sandia’s simulation packages and supercomputing resources to address statistical problems arising from atomistic simulations of low-probability events, such as transport of hydrogen through solid materials containing defects.

The aim of HyMARC is to not only accurately simulate all possible reactions that could occur during the hydriding / dehydriding process using atomistic simulations, but also to generalize our methodologies to enable them to be quickly adapted to new materials. This requires us to develop new interatomic potentials for storage materials that have not been considered in the literature, and to improve the accuracy of existing potentials that usually cannot model chemical reactions and phase transformations. We have developed a variety of interatomic potentials that achieved this including the embedded atom method potential database involving 16 elements1, the polymorphic interatomic potential,2 the potential incorporating the reactive interaction between helium and metals containing hydrogen isotopes,3,4 and various hydrogen-containing analytical bond order potentials (BOP).5-17 Analytically derived from quantum-mechanical calculations,8-12 the fidelity of BOP has been demonstrated for a number of materials, including CdZnTe,13,14 Al-Cu,15 Cu-H,16 and C.17 As an example, our carbon BOP17 enables molecular dynamics (MD) simulations to capture various atomic reactions between carbon vapor and a copper surface, which results in the correct prediction graphene growth on copper (Figure 1).

Statistics are another challenge for atomistic simulations because an alloy with a given composition can have countless distinct atomic populations on lattice sites. This impacts all thermodynamic and kinetic properties. Using kinetic properties as an example, in the past, atomistic calculations of diffusion energy barriers were usually computed for each atomic jump path. Practical materials often involve thousands of distinct atomic jump paths that are not known a priori. The problem is compounded during hydriding and dehydriding processes, in which the structure is evolving including formation of various. Even if all atomic jump paths are considered, it is still unclear how thousands of atomic jump events are related to the overall diffusion behavior seen in experiments. Sandia’s large-scale computing resources allow us to determine an overall diffusion energy barrier and an overall pre-exponential factor from the Arrhenius equation constructed from MD simulation of the mean-square displacement of the diffusing species at different temperatures18-23. An example of the Arrhenius plots obtained from such MD simulations of hydrogen diffusion in palladium19 is shown in Fig. 2. The highly converged linear Arrhenius plots validate that the overall diffusion energy barrier accounting for all atomic jump paths can be accurately determined. They also validate that atoms are able to move around and reach dynamical equilibrium during MD simulations.

Figure 1. technical illustration

Figure 1. Molecular dynamics simulation of graphene growth on copper. Large golden balls: copper; small red balls: initial graphene island; blue balls: deposited carbon graphene

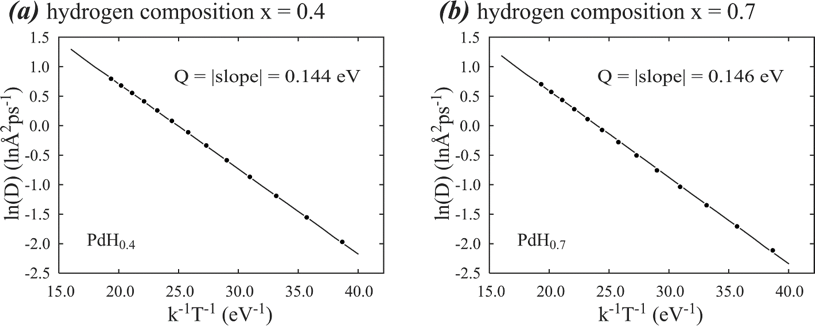
Figure 2 technical Illustration

Figure 2. Arrhenius plots of hydrogen diffusion in two palladium hydrides of (a) PdH0.4 and (b) PdH0.7.

Fig. 3 shows another example where statistical problems have been well addressed using large scale MD. Here hydrogen concentration profiles around an edge dislocation (Cottrell atmosphere) in aluminum are calculated using time and ensemble averaged MD simulations. Normally, if a system contains few hydrogen atoms, then snapshot of configuration is discrete, only the sites of hydrogen have a 100% concentration but all other sites have a zero concentration. This cannot represent a smooth concentration profile. However, by using time and averaged MD simulations, the hydrogen Cottrell atmosphere shown in Fig. 3 are very smooth. Compared with Monte Carlo method previously used to study Cottrell atmosphere, MD is more accurate as it does not involve approximations other than the interatomic potential. In addition, MD allows the study of kinetic process even when dislocations migrate under external stresses (or structures evolve during hydrogenation), which cannot be studied using previous approaches. Because atoms stay for the correct residence time at each lattice site they visit during an MD simulation, performing a large number of time-averaged simulations can resolve the statistical issue of atomistic simulations, provided that sufficient computing resources are available.24

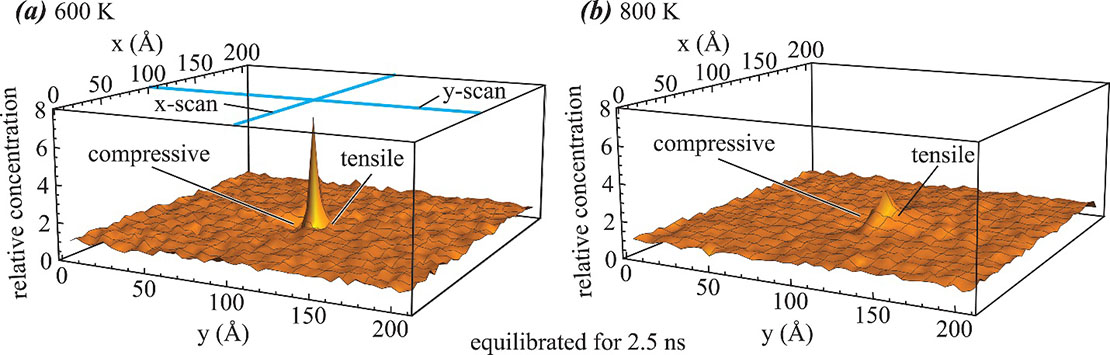
Figure 3 technical illustration

Fig. 3. Hydrogen Cottrell atmosphere around an edge dislocation in aluminum obtained from time and ensemble averaged MD simulations: (a) T = 600 K and (b) T = 800 K.

Sandia has also developed large scale kMC methods to simulate structure evolution at large time and length scales.25-27

Status

Available for use in collaboration with HyMARC.

References

  1. X. W. Zhou, R. A. Johnson, and H. N. G. Wadley, Phys. Rev. B, 69, 144113 (2004).
  2. X. W. Zhou, R. E. Jones, and K. Chu, J. Appl. Phys., 122, 235703 (2017)
  3. X. W. Zhou, N. C. Bartelt, and R. B. Sills, Phys. Rev. B, 103, 014108 (2021).
  4. X. W. Zhou, M. E. Foster, and R. B. Sills, J. Nuc. Mater., 575, 154232 (2023).
  5. X. W. Zhou, M. E. Foster, J. A. Ronevich, and C. W. San Marchi, J. Comp. Chem., 41, 1299 (2020).
  6. X. W. Zhou, D. K. Ward, and M. E. Foster, New J. Chem., 42, 5215 (2018).
  7. X. W. Zhou, S. Kang, T. W. Heo, B. C. Wood, V. Stavila, and M. D. Allendorf, ChemPhysChem, 20, 1 (2019).
  8. D. G. Pettifor, M. W. Finnis, D. Nguyen-Manh, D. A. Murdick, X. W. Zhou, and H. N. G. Wadley, Mater. Sci. Eng. A, 365, 2 (2004).
  9. D. G. Pettifor, I. I. Oleinik, Phys. Rev. Lett., 84, 4124 (2000).
  10. D. G. Pettifor, I. I. Oleinik, Phys. Rev. B, 65, 172103 (2002).
  11. R. Drautz, D. Nguyen-Manh, D. A. Murdick, X. W. Zhou, H. N. G. Wadley, and D. G. Pettifor, TMS Lett., 1, 31 (2004).
  12. R. Drautz, D. A. Murdick, D. Nguyen-Manh, X. W. Zhou, H. N. G. Wadley, and D. G. Pettifor, Phys. Rev. B, 72, 144105 (2005).
  13. D. K. Ward, X. W. Zhou, B. M. Wong, F. P. Doty, and J. A. Zimmerman, Phys. Rev. B, 85, 115206 (2012).
  14. D. K. Ward, X. W. Zhou, B. M. Wong, and F. P. Doty, J. Mol. Model, 19, 5469 (2013).
  15. X. W. Zhou, D. K. Ward, and M. E. Foster, J. Alloys Comp., 680, 752 (2016).
  16. X. W. Zhou, D. K. Ward, M. E. Foster, and J. A. Zimmerman, J. Mater. Sci., 50, 2859 (2015).
  17. X. W. Zhou, D. K. Ward, and M. E. Foster, J. Comp. Chem., 36, 1719 (2015).
  18. X. W. Zhou, F. El Gabaly, V. Stavila, and M. D. Allendorf, J. Phys. Chem., 120, 7500 (2016).
  19. X. W. Zhou, T. W. Heo, B. C. Wood, V. Stavila, S. Kang, and M. D. Allendorf, Script Mater., 149, 103 (2018).
  20. X. W. Zhou, Dingreville, and R. A. Karnesky, Phys. Chem. Chem. Phys., 20, 520 (2018).
  21. R. Skelton, X. W. Zhou, and R. A. Karnesky, J. Nuc. Mater., 555, 153099 (2021).
  22. C. D. Spataru,T. W. Heo, B. C. Wood, V. Stavila, S. Kang, M. D. Allendorf, and X. W. Zhou, Phys. Rev. Mater., 4, 105401 (2020).
  23. R. Skelton, C. Nowak, X. W. Zhou, R. A. Karnesky, J. Nuc. Mater., 565, 153765 (2022).
  24. X. W. Zhou, T. W. Heo, B. C. Wood, V. Stavila, S. Kang, and M. D. Allendorf, J. Appl. Phys., 123, 225105 (2018).
  25. S. Plimpton, C. Battaile, M. Chandross, L. Holm, A. Thompson, V. Tikare, G. Wagner, E. Webb, X. Zhou, C. Garcia Cardona, and A. Slepoy, Sandia report SAND2009-6226, October 2009.
  26. http://spparks.sandia.gov
  27. X. W. Zhou, R. A. Karnesky, N. Yang, and J. K. Yee, Comp. Mater. Sci., 179, 109605 (2020).